quinta-feira, 18 de junho de 2009
Divisão
1° caminho: REPARTINDO
Podemos encontrar o resultado de algumas divisões de frações utilizando a idéia de repartir.
Por exemplo, se repartimos de uma barra de chocolate entre 2 crianças, cada uma receberá a metade de da barra:
Então, o resultado da divisão de por 2 é . Escrevemos: .
2° caminho: QUANTAS VEZES CABE?
Em outros casos encontramos o resultado verificando quantas vezes um número cabe no outro.
Com números naturais estamos acostumados a fazer isto. Por exemplo, se queremos achar o resultado de 8 dividido por 4, procuramos quantas vezes 4 cabe em 8. Como 4 cabe 2 vezes em 8 (2 x 4 = 8), dizemos que 8 : 4 = 2.
Podemos aplicar esta idéia a frações. Quando procuramos o resultado de , estamos querendo saber quantas vezes cabe em . Um desenho responde imediatamente:
Então podemos escrever:
Como se pode perceber, as idéias de "repartir" e de "quantas vezes cabe" são equivalentes. É uma questão de se achar mais fácil ou mais difícil usar cada uma delas, em cada caso.
Propriedades da multiplicação
Associatividade: O agrupamento dos fatores não altera o resultado. Assim, se (x . y) . z = w, logo x . (y . z) = w.
Distributividade: Um fator colocado em evidência numa soma dará como produto a soma do produto daquele fator com os demais fatores. Assim, x . (y + z) = (x . y) + (x . z).
Elemento neutro: O fator 1 (um) não altera o resultado dos demais fatores. O um é chamado "Elemento neutro" da multiplicação. Assim, se x . y = z, logo x . y . 1 = z.(obs:o 0 é o da soma.)
Elemento opositor: O fator -1 (menos um) transforma o produto em seu simétrico. Assim, -1 . x = -x e -1 . y = -y, para y diferente de x.
Fechamento: O produto de dois números reais será sempre um número real.
Anulação: O fator 0 (zero) anula o produto. Assim, x . 0 = 0, e y . 0 = 0, com x diferente de y.
Na matemática , podemos dizer que a multiplicação é a mais simples formar de agruparmos uma quantidade finita de números.Ao efeturmaos uma multiplicação , chegamos a uma resposta que é chamada de PRODUTO.Na geometria , está relacionada tembém como uma operação geométrica - a partir de dois segmentos de retas dados, podemos determinar um outro cujo comprimento seja igual ao produto dos dois inciais.
Subtração
Uma subtração é representada por:
é o minuendo, é o subtraendo, é a diferença.
A subtração é o mesmo que a adição por um número de sinal inverso. É, portanto, a operação inversa da adição.
Propriedades da adição
Comutatividade: A ordem das parcelas não altera o resultado final da operação. Assim, se x + y = z, logo y + x = z.
Associatividade: O agrupamento das parcelas não altera o resultado. Assim, se (x + y) + z = w, logo x + (y + z) = w.
Elemento neutro: A parcela 0 (zero) não altera o resultado das demais parcelas. O zero é chamado "elemento neutro" da adição. Assim, se x + y = z, logo x + y + 0 = z.
Fechamento: A soma de dois números reais será sempre um número real.
Anulação: A soma de qualquer número e o seu oposto é zero. Exemplo:
* 2 + (-2) = 0
* (-999) + 999 = 0
aerodinamica.
De uma forma geral, a aerodinâmica, como ciência específica, só passou a ganhar importância industrial com o surgimento dos aviões e dos automóveis pois estes precisavam se locomover tendo o menor atrito possível com o ar pois assim seriam mais rápidos e gastariam menos combustível.
O estudo de perfis aerodinâmicos, ou aerofólios, provocou um grande salto no estudo da aerodinâmica. Neste início o desenvolvimento da aerodinâmica esteve intimamente ligado ao desenvolvimento da hidrodinâmica que apresentava problemas similares, e com algumas facilidades experimentais, uma vez que já havia tanques de água circulante na época embora não houvesse túneis de vento. George Cayley é considerado o Pai da Aerodinâmica.
Forças da aerodinâmica da aviação
[editar] Peso
O peso é uma força que é sempre dirigida para o centro da terra: trata-se da força da gravidade. A magnitude desta força depende de todas as partes do avião, mais a quantidade de combustível, mais toda a carga (pessoas, bagagens, etc.). O peso é gerado por todo o avião. Mas nós podemos simplesmente imaginá-la como se atuasse num único ponto, chamado centro de gravidade. Em vôo, o avião gira sobre o centro de gravidade, e o sentido da força do peso dirige-se sempre para o centro da terra. Durante um vôo, o peso do avião muda constantemente à medida que o avião consome combustível. A distribuição do peso e do centro de gravidade pode também mudar, e por isso o piloto deve constantemente ajustar os controles, ou transferir o combustível entre os depósitos, para manter o avião equilibrado.
[editar] Sustentação
Para fazer um avião voar, deve ser gerada uma força para compensar o peso. Esta força é chamada sustentação e é gerada pelo movimento do avião através do ar. A sustentação é uma força aerodinâmica ("aero" significa ar, e " dinâmica" significa movimento). A sustentação é perpendicular (em ângulo reto) ao sentido do vôo. Tal como acontece com o peso, cada parte do avião contribui para uma única força de sustentação, mas a maior parte da sustentação do avião é gerada pelas asas. A sustentação do avião funciona como se atuasse num único ponto, chamado centro de pressão. O centro de pressão é definido tal como o centro de gravidade, mas usando a distribuição da pressão em torno de toda a aeronave, em lugar da distribuição do peso. Além do centro de pressão, outro ponto no aerofólio é de grande importância no projeto de uma aeronave: o centro aerodinâmico. Neste, o coeficiente de momento não varia quando variamos o ângulo de ataque. O coeficiente de momento é um coeficiente adimensional que qualifica e quantifica se, para certo aerofólio, há um momento picante ou cabrante sobre o engaste da asa. Este momento é fundamental, por exemplo, na determinação das cargas aerodinâmicas para definição da estrutura e para o projeto de sistemas de controle, como o profundor.
[editar] Arrasto
À medida que o avião se move através do ar, há uma outra força aerodinâmica presente. O ar resiste ao movimento do avião, e esta força de resistência é denominada arrasto (ou atrito). Tal como a sustentação, há muitos fatores que afetam a magnitude da força de arrasto, como a forma do avião, a viscosidade do ar e a velocidade. E tal como acontece com a sustentação, consideram-se usualmente todos os componentes individuais como se estivessem agregados num único valor de arrasto de todo o avião. O sentido da força de arrasto é sempre oposto ao sentido do vôo, e o arrasto atua através do centro de pressão.
Quando um avião aumenta o ângulo de ataque, aumenta também a sustentação; mas há uma geração de gradientes de pressão adversos. À partir de um certo ângulo de ataque, estes gradientes de pressão adversos resultam no descolamento da camada limite, cuja geração de vórtices de von Kárman caracteriza o fenômeno conhecido como estol. No estol, perde-se sustentação, e o arrasto aumenta significantemente. É por este fato que, na fase de decolagem de um aeromodelo, não se deve fazê-lo subir em ângulo muito acentuado. Algumas aeronaves, principalmente aquelas com projeto de calda em T, correm o risco de sofrerem "deep stall" (estol profundo), pois a esteira gerada na asa durante o estol cobre o estabilizador horizontal, fazendo-a perder capacidade de controle e impedindo que a aeronave retorne para sua atitude inicial. Por este motivo, além disso, aeronaves acrobáticas devem possuir um projeto de empenagem que garanta a saída do estol e parafuso. Aeronaves com sistemas de controle mais complexos, como os caças e jatos comerciais, em geral possuem sistemas automáticos para proteção de estol, como o "shaker" e o "pusher".
Volume
O volume de um corpo é a quantidade de espaço ocupada por esse corpo. Volume tem unidades de tamanho cúbicas (por exemplo, cm³, m³, in³, etc.) Então, o volume de uma caixa (paralelepípedo retangular) de comprimento T, largura L, e altura A é:
V = T x L x A
Sua unidade no Sistema internacional de unidades é o metro cúbico (m³). A seguinte tabela mostra a equivalência entre volume e capacidade.
Fórmulas do volume
Fórmulas comuns para o cálculo do volume de sólidos:
- Cubo:
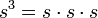 (onde s é o comprimento de um lado)
(onde s é o comprimento de um lado) - Paralelepípedo:
 (largura, comprimento, altura)
(largura, comprimento, altura) - Cilíndro:
 (r = raio de uma face circular, h = altura)
(r = raio de uma face circular, h = altura) - Esfera:
 (r = raio da esfera)
(r = raio da esfera) - Elipsóide:
 (a, b, c = semi-eixos do elipsoide)
(a, b, c = semi-eixos do elipsoide) - Pirâmide:
 (A = área da base, h = altura)
(A = área da base, h = altura) - Cone:
 (r = raio do círculo na base, h = altura)
(r = raio do círculo na base, h = altura) - Prisma:
 (A = área da base, h = altura)
(A = área da base, h = altura) - Qualquer figura

onde h é qualquer dimensão da figura, e A(h) é a área da intersecção perpendicular para h descrita pela função da posição ao longo de h.
Cálculo integral
Para o cálculo de volumes é possível utilizar-se integrais com duas variaveis. A tabela seguinte apresenta alguns exemplos:
| Sólido | Integral | Onde |
|---|---|---|
| Esfera | 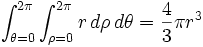 |  : raio : raio |
| Paralelepípedo |  | 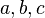 : dimensões das arestas : dimensões das arestas |
Tipos de fração
- própria: o numerador é menor que o denominador. Ex.:

- imprópria: o numerador é maior que o denominador. Ex.:

- mista: constituída por uma parte inteira e uma fracionária. Ex.:
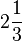 .Pode-se encontrar uma fração imprópria a partir do número misto:
.Pode-se encontrar uma fração imprópria a partir do número misto: 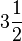 2x3=6 6+1=7 (7=numerador/2=denominador)e assim por diante repetindo o denominador
2x3=6 6+1=7 (7=numerador/2=denominador)e assim por diante repetindo o denominador
- aparente: é quando o numerador é múltiplo ao denominador. Ex.:

- equivalentes: aquelas que mantêm a mesma proporção de outra fração. Ex.:
 4 e 4 dividos por 2(ou outro número) é igual a 2.
4 e 4 dividos por 2(ou outro número) é igual a 2.
- irredutível: o numerador e o denominador são primos entre si, não permitindo simplificação. Ex.:

- unitária: o numerador é igual a 1 e o denominador é um inteiro positivo. Ex.:

- egípcia: fração que é a soma de frações unitárias, distintas entre si. Ex:
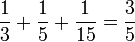
- decimal: o denominador é uma potência de 10. Ex.:

- composta: fração cujo numerador e denominador são frações:
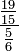
- contínua: fração constituída a partir de uma sequência de inteiros naturais (a0,a1,a2,a3,...,ak,...) da seguinte maneira

